Myśleć funkcyjnie #2
System typów
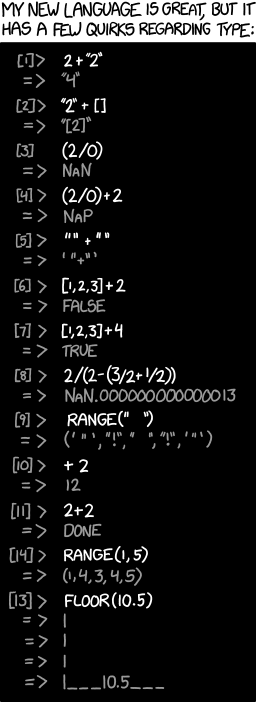
Retrospekcja
() :: ()
[1,2,3,4,5] :: Num t => [t]
"Wąchock & 漢字" :: [Char]
(10, "Karmel") :: Num t => (t, [Char])
(True, -1) :: Num t => (Bool, t)
[(1,"San Francisco"), (2, "New York")] :: Num t => [(t, [Char])]
(:) :: a -> [a] -> [a]
[] :: [a]
head :: [a] -> a
tail :: [a] -> [a]
take :: Int -> [a] -> [a]
filter :: (a -> Bool) -> [a] -> [a]
map :: (a -> b) -> [a] -> [b]
foldr :: (a -> b -> b) -> b -> [a] -> b
foldl :: (a -> b -> a) -> a -> [b] -> a
odd :: Integral a => a -> Bool
even :: Integral a => a -> Bool
div :: Integral a => a -> a -> a
mod :: Integral a => a -> a -> a
(&&) :: Bool -> Bool -> Bool
(||) :: Bool -> Bool -> Bool
(==) :: Eq a => a -> a -> Bool
(/=) :: Eq a => a -> a -> Bool
sqrt :: Floating a => a -> a
print :: Show a => a -> IO ()
sqr :: Num a => a -> a
(>:) :: [a] -> a -> [a]
lessthan8 :: (Num a, Ord a) => a -> Bool
(5+) :: Num a => a -> a
wybierz :: Num a => (a -> a -> Bool) -> a -> a -> a
polityka1 :: Ord a => a -> a -> Bool
bank1_wybierz :: (Num a, Ord a) => a -> a -> a
Dane
Aliasy
-- alias
type String = [Char]
-- "bardziej skryty" alias
newtype Money = Money Integer
"Dane"
-- typ parametryzowany
data Maybe a = Nothing | Just a
data Either a b = Left a | Right b
-- własne dane
data Kolory = Czerwony | Zielony | Niebieski
-- mogą być parametryzowane i rekurencyjne
data Drzewo a = Nic | Węzeł a (Drzewo a) (Drzewo a)
Zadania
Zadanie: Stworzyć własny typ danych, który reprezentuje kolory
Klasy
Klasy grupują operacje, które można wykonać na danych (mogą zawierać domyślną implementację):
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x /= y = not (x == y)
Klasy mogą zależeć od siebie:
class (Eq a) => Ord a where
(<) :: a -> a -> Bool
(>=) :: a -> a -> Bool
-- itd.
GHCI i typy raz jeszcze
Aby wyświetlić typ wyrażenia w GHCI trzeba poprzedzić je komendą :t albo przestawić flagę :set +t.
Aby wyświetlić więcej informacji, np. zobaczyć zdefiniowane instancje klas, w GHCI trzeba poprzedzić je komendą :i.
Np. aby zobaczyć wszystkie typy danych, którym można sprawdzać równość, wystarczy wywołać:
:i Eq
Implementowanie klasy
Automatyczna implementacja niektórych klas:
data Maybe a = Nothing | Just a deriving (Eq, Ord, Read, Show)
-- wymaga :set -XGeneralizedNewtypeDeriving
newtype Money = Money Integer deriving (Eq, Ord, Num)
Ręczna implementacja klas:
instance Num a => Num (Maybe a) where
Nothing + _ = Nothing
_ + Nothing = Nothing
(Just x) + (Just y) = Just (x + y)
-- uwaga: niepełna definicja, tylko jedna operacja jest zdefiniowana!
Just 1 + Just 2
-- Just 3
Nothing + Just 4
-- Nothing
Ważne: można nakładać ograniczenia kontekstu w definicji danych, ale w praktyce unika się tego i stosuje ograniczenia wyłącznie na funkcjach, które go potrzebują lub w definicjach klas.
Zadania
Zadanie: Zaimplementować operację dodawania z klasy Num dla naszego nowego typu przechowującego kolory
Standardowe klasy Haskela 98
Ilustracja prosto z Haskell 98 Online Report.
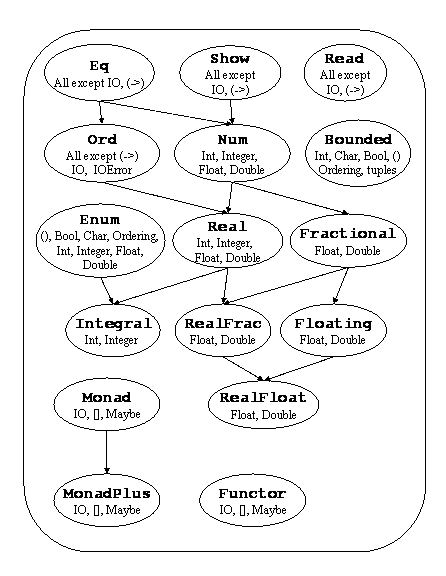
Historycznie Funktory i Aplikatory, o których za chwilę, zostały wprowadzone do języka później, niż Monady, dlatego hierarchia wyglądała inaczej.
W GHC 7.10 (27 marca 2015) została wprowadzona propozycja Applicative Monad.
Funktory
Na instancjach tej klasy można wywoływać "gołe" funkcje za pomocą fmap
class Functor f where
fmap :: (a -> b) -> f a -> f b
Dla list implementacja fmap to po prostu map. fmap jest ogólniejszą koncepcją.
Implementacja funktorów powinna spełnić pewne właściwości, które jednak są wymagane jedynie przez konwencję
fmap id == id
fmap (f . g) == fmap f . fmap g
Zadania
Zadanie: Mając typ danych data Drzewo a = Nic | Węzeł a (Drzewo a) (Drzewo a) zaimplementować dla niego instancję funktora
Maybe
data Maybe a = Nothing | Just a
instance Functor Maybe where
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)
fmap (\x -> x*x) (Just 5)
fmap (\x -> x*x) Nothing
Więcej Maybe
Maybe jest jednym z podstawowych narzędzi i standardowa biblioteka posiada kilka bardzo przydatnych funkcji pomocniczych, które siedzą w module Data.Maybe, np.:
maybe :: b -> (a -> b) -> Maybe a -> b
lookup :: Eq a => a -> [(a, b)] -> Maybe b
catMaybes :: [Maybe a] -> [a]
mapMaybe :: (a -> Maybe b) -> [a] -> [b]
Przykład użycia... napiszecie sami!
newtype Ident = Ident Int deriving Eq
type Login = String
type Baza = [(Ident, Login)]
data Użytkownik = Niezarejestrowany | Znany Login deriving Show
-- znajdź :: Ident -> Baza -> Użytkownik
-- znajdź :: Baza -> Ident -> Użytkownik
-- znajdź ??? = ???
main = print $ znajdź (Ident 3) [(Ident 3,"Ala")]
Either
"You Either have a Right answer or you're Left with an error."
data Either a b = Left a | Right b
fmap (\x -> x*x) (Right 5)
fmap (\x -> x*x) (Left "Failed")
Więcej Either
Either również posiada zestaw funkcji pomocniczych, analogicznie w Data.Either, np.:
either :: (a -> c) -> (b -> c) -> Either a b -> c
lefts :: [Either a b] -> [a]
rights :: [Either a b] -> [b]
partitionEithers :: [Either a b] -> ([a], [b])
Aplikatory
Aplikator rozszerza koncepcje zamkniętą w Funktorze. Teraz można również funkcje zamknięte w instancji tej klasy zaaplikować na wartościach w niej zamkniętych
class Functor f => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
Dodatkowo jest też zdefiniowany alias: (<$>) = fmap.
pure (+) <*> [1,2,3] <*> [1,2,3]
(+) `fmap` [1,2,3] <*> [1,2,3]
(+) <$> [1,2,3] <*> [1,2,3]
Implementacja aplikatora zapewnia nam, że możemy komponować funkcje z danymi zamkniętymi w "pudełkach" bez wcześniejszego ich "odpakowywania".
Oczywiście aplikatory również powinny posiadać pewne właściwości:
-- identity
pure id <*> v == v
-- composition
pure (.) <*> u <*> v <*> w == u <*> (v <*> w)
-- Bez aplikatora: (u . v) w == u (v w)
-- homomorphism
pure f <*> pure x == pure (f x)
-- interchange
u <*> pure y == pure ($ y) <*> u
-- Bez aplikatora: u y == ($ y) u
Przykład z wcześniej, czyli dlaczego nie potrzebujemy domyślnej implementacji Num (Maybe a):
(+) <$> Just 1 <*> Just 2
(+) <$> Nothing <*> Just 4
Zadania
Zadanie: Bazując na poprzedniej implementacji, zapisać dla typu Drzewo instancję aplikatora. Żeby sprawdzić działanie - dodajcie do siebie wartości zawarte w dwóch drzewach (wynikiem jest drzewo).
Interludium
